Límites.
LÍMITES
El límite de una función de variable real es un concepto fundamental del análisis matemático aplicado a las funciones. Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente próximos a c, sin importar el valor que pudiera adquirir f en el punto c.
Límite de una función
 tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función  tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
El límite de una función f(x), cuando x tiende a c es L si y sólo si para todo  existe un
existe un 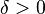 tal que para todo número real x en el dominio de la función
tal que para todo número real x en el dominio de la función  .
.
 existe un
existe un 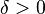 tal que para todo número real x en el dominio de la función
tal que para todo número real x en el dominio de la función  .
.En éste temario se aprenderá:
- Solución de Límites Algebraicos Fraccionarios
- Solución de Límites Algebraicos
Límite Algebraico Fraccionario
Visualización de los parámetros utilizados en la definición de límite Graf. 1
Límites Polinómicos
Función en Geogebra
Límites con Raíces Cúbicas
Límites con Raíz Cúbica
Gracias a Luis Felipe
Límites Trigonométricos
.
Ésta plataforma se basa y agradece a Julio Ríos profesor web que facilita la enseñanza a sus seguidores
Cali-Colombia
Luis Felipe










Comentarios
Publicar un comentario